
みなさん、こんにちは!スタッキーです。
算数で「つるかめ算」や「旅人算」を習いましたが、今でも解き方を覚えてますか?
わたしは全く覚えていませんでした。もしかしたら、名前だけ覚えて終わりにしたかもw
そんなわが家にも、とうとう奴らが土足でやってくるようになりました。
しかも、どんでもない種類の多さです。いつの間にこんなに増えていたのかと思うほどです。
それと同時に弱点をつぶすのがとても難しい分野なのだということも分かってきました。
今回は、わが家で実施した一点突破学習「文章題」についてお伝えしたいと思います。
この記事は次のような人におすすめ!
・算数を得意科目にするために「文章題」を攻略したい
・子どもが間違えた箇所が把握できないために学習ロスが発生している
・実践問題や応用問題になると点数が取れずどうしたら良いか困っている
・できれば自分で弱点を見つけて専門家に質問してきてほしい
文章題に取り組むなら最初に「可視化のテクニック」を手に入れましょう!
それではどうぞ!
※当ブログでは商品・サービスのリンク先にプロモーションを含みます。ご了承ください。
問題を反復練習するだけでは賢くならない
闇雲に解いて答えが当たるパターンが危険

たまに子どもが「先生やテキストの通りやったら問題が解けた」と言ってくることがあります。
これには思わぬ落とし穴があり、放置するとスコアがガッツリさがって意気消沈することも。
また、黙々と問題を解きまくり「終わったー」っと言ってくる時も同様に危険です。
なぜなら、問題個別に解き方を暗記して数字をはめ込む作業をしていることがあるからです。
少しでも問題がアレンジされたら、本人も気づかない間に瞬殺される恐れがあります。
そこで、あやしいと感じた時は問題用紙を見て図や式の具合を確認してみることにしました。
「さっそく発見しました!いきなり数式パターンです!」
コレを見つけたらほぼアウトです。勉強している雰囲気だけなので一度寝かせてあげましょう。
本人に悪気はないと思います。我々が倒すべきは敵は「文章題の闇」一点です。
どこで間違えたかを特定する仕組みがない
むつかしい問題では回答解説の意味が分かっても自分が間違えたポイントは特定できません。
もし、この状態で解きなおしを行うと、先程と同様に数字はめ込み作業が再来してしまいます。
これが発生する原因は、自分が問題を解いている時に考えた手順が残っていないからです。
しかし、どのようにすれば考えた手順をあとで見れるようにすることができるのでしょうか。
思考の過程を全部文字にするわけにもいかないですし、録音で間違った答えを覚えられるのも。。
このムツカシイ状況を早く脱したい。それがこの実験をはじめようと思ったキッカケです。
そう、今回のテーマは「文章題の闇」に光をあてる「可視化のテクニック」です。

文章題を解く3つのステップを可視化する
① 問題文を分析して情報を書き込む

テストで問題文を2度読んでしまうと問題を解くために使える時間がかなり圧迫されます。
そのため、一発で問題文を読んで状況を理解し、回答を導くルートを探し出す必要があります。
しかし、急ぐあまり思考のステップを飛ばしてしまっては元も子もありません。
そこで、いくつかの重要な点を確実に押さえて「探し読みするトレーニング」をしてみます。
この「探し読み」における可視化のテクニックは以下のような点です。
①状況:状況が変化するポイントで区切り線(/)を入れて状況番号(例:①)をつける
②回答:問われていることに下線を引き、単位にマルをする
③解法:解き方のアプローチを仮決めしてカタカナ(例:タビビト)で書く
④情報:値や割合などの情報に下線を引く
※割合の場合は「基にする数と比べる数」を含めて線を引く(例:仕入れ値の3割の利益)
手を動かしながら問題文を読むことで、必要な情報を確実に拾えるように訓練していきます。
慣れてきたら図や表を整理しながらということもできるかもしれませんが、ココは我慢です。
あたり前とも思えるこの動作が漏れたことで失われるスコアが非常に多いからです。
それぞれのステップでイメージすべきことはもう少し多いのですが、まずは基本からです。
このようにすることで最低限のステップを理解し、その足跡を問題文に残すようにしました。
② イメージを使って状況を整理する

文章題で唯一わたしが気に入っている点をあげるとすれば図がバリバリ登場するところです。
世の中には「方程式」というものがあり、あんまり考えずに答えが出せる便利なツールです。
ただ、正直、トロい。。
やっぱり、右脳を使って問題を解いていく方が圧倒的にインテリジェントで高速なのです。
ということで、図・グラフ・表などは、駆使できるようにしておきたいところです。
②意外と便利な「整理表」を正確に使えるようにする
③特定の問題で重宝する「グラフ」を理解して
①「線分図」と「面積図」は、使い方を徹底的にマスターしておくべき図といえるでしょう。
いずれも広範囲な文章題をカバーしており、特徴をおさえれば算数の強力な武器となります。
図の作成における可視化のテクニックは次のような点です。
- 状況ごとに図が書き分けられているか(状況番号を記入)
- 与えられた値がすべて記入されているか(情報を記入)
- 問われていることが記入されているか(□などで記入)
- 実数と割合が上下に分けて記入できている
- 実数の単位が記入されているか
- 割合は元となる数と比べる数を同じ記号でグループ化できているか
最初はこれらの情報を正確に記入して、きちんと考えるための準備を整えるようにします。
子どもはすぐに省略しようとする傾向があるので、鬼の形相で見守ってあげましょうW
②「整理表」は、「濃度算」などの3公式系問題で使うツールでコレだけでも相当に便利です。
表を作った時点で答えがでることもあるので、ぜひマスターしておきたいですね。
この整理表をマスターするコツは、見出しを固定して毎回同じように数字を埋めることです。
そして、問題の難易度に応じて使い方がどのように変化するか経験を重ねることにつきます。
整理表の作成における可視化のテクニックは次のような点です。
- 整理表の見出しが漏らさず記入できているか
- 問題文の状況を正確に図表に記入していけるか(状況番号を記入)
- 与えられた値がすべて記入されているか(情報を記入)
- タテ、ヨコの関係から数字を埋め込めているか
- 表の中に記入した式が正しいか
③「グラフ」の読み取りは、「旅人算」や「容器と水量の関係」などでは必須です。
特に旅人算の折り返し系問題ではグラフを線分上に投影するとあっさりトケルことが多いです。
そんなにパターンも多くないので、状況を丁寧に読み取る練習をしましょう。
グラフの読み取りにおける可視化のテクニックは次のような点です。
- グラフのタテ軸とヨコ軸の単位を把握しているか(マルで囲む)
- グラフ上の点についてタテとヨコの数字を書き込めるか(数字を記入)
- 状態の変化をグラフ上に書き込めるか(状態番号を記入)
- 傾きに値を記入できているか
③ 言葉の式を意識して立式する
せっかく図を作成して回答を導くルートが見えても最後に数字あそびのワナが待っています。
答えを出さなければという焦りから、立式がずさんになり回答までの思考をゆがめるのです。
功を焦るとロクなことがないのでココもじっくりと進めたいところです。
そこで、図から式に移る前に回答を導くルートが正しいか可視化しておきたいと思います。
そのために使うのが「言葉の式」です。
立式に必要な「同じ」つまり「=」で結ばれる2つのモノを書き出す専用のトレーニングです。
言葉自体は稚拙であっても認識があっていて立式できる内容ならヨシとしましょう。
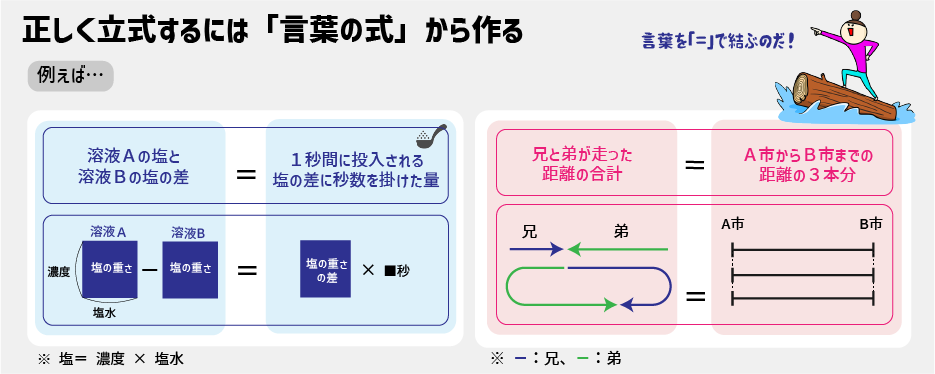
「言葉の式」を用いた可視化のテクニックでは次のような文章を作ります。
「溶液Aの塩と溶液Bの塩の差」が「1秒間に投入される塩の差に秒数を掛けた量」と同じ。
「お兄さんと弟が走った距離の合計」が「A市からB市までの距離の3本分」と同じ。
これで、立式において着眼ポイントが間違っていれば、容易に修正できるようになりました。
正確無比の爆弾処理トレーニング
計算の種別を絞り込んで罠を回避する
大人たちが作るテストの問題は子どもが全員とけてしまうと意味を失う性質があります。
そのため、間違いを誘うギミックや遅延を引き起こすトリックが方々に散りばめられています。
計算1つとっても、四則演算、少数や分数などの数値、括弧の種別、還元算など罠だらけです。
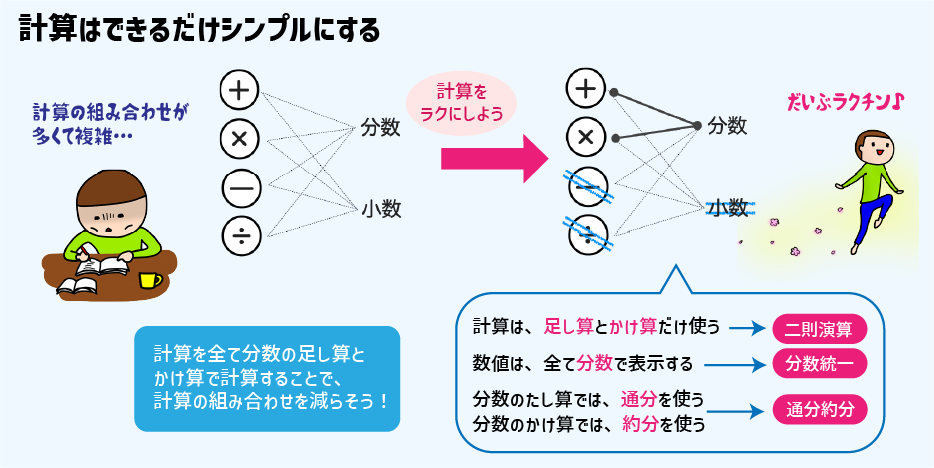
そこで、「二則演算」と「分数統一」を中心に計算テクニックを収斂させます。
まず、四則演算と数値ですが、この組み合わせだけでも8通りになってしまいます。
そこで、これらの罠を回避するために計算を極力シンプルにしていくことを考えてみます。
よほど特殊な問題でない限り、少数や割合は「分数」に置き換えて表現することができます。
帯分数も一旦すべて仮分数に寄せてしまってよいでしょう。
そして、割り算は「掛け算」に、引き算は「足し算」に置き換えて二則演算にしてしまいます。
これで、計算を「分数の掛け算」と「分数の足し算」に集約し、種別を4分の1に減らします。
そして、この2つの計算で頻繁に登場する「通分」と「約分」を徹底的に鍛え上げます。
しかし、その中身は「倍数」と「約数」であることに気づくでしょう。
次に、括弧の種別や還元算ですが、こちらに関しては便利ツール「方程式」の出番です。
文章題ではあまり力を発揮できない「方程式」ですが、式の変形に関しては最強といえます。
特に、子どもがミスしやすい括弧の展開や還元算の対応などは朝飯前です。
そこで、方程式を用いて「分配法則」や「移項」などの式変形テクニックをつぶし込みます。
そして、最後まで「筆算」を使うような計算はしない努力をしていきます。
計算量を減らすことで間違いを避ける

ある程度、式変形や通分/約分が進むといよいよ計算するべきフェーズがやってきます。
しかし、ココでもやはり計算をできる限りしない方向に倒したいところです。
そのために使えるのは、計算をラクにする「工夫計算」計算をなくす「数字暗記」です。
まず、「平方数」「2桁かけ算」「3.14(π)」などはまとめて暗記するのがおススメです。
実際に列挙して眺めてみると分かるのですが、九九ほど覚える個数は多くありません。
その割には恐ろしいほどの頻度で問題に登場してきます。
となれば、計算の完全消滅を図るべく覚えておきたくなりますね。コスパは最強です。
わが家の格言「計算しなければ間違えない」に最も近い存在がこの数字暗記だと思います。
下記の学習マテリアルにて数字暗記のチートシートを配布しています。
よろしければ、お子様の算数教科に活用ください。
「学習マテリアル」の記事一覧では、円周率や平方数、2けたかけ算、割合などのチートシートをはじめ、学習に役立つマテリアルを提供しています。
次に、「工夫計算」ですが、こちらは代表的なモノを使えるようにしておけばよいでしょう。
その中でも重要なものには、「足して〇になる数」「掛けて〇になる数」があります。
特に「掛けて〇になる数」は「割合」や「逆数」の理解も進むので良いですね。
この辺りは、要望があればチートシートを作ってみたいと思います。
とはいえ、計算力は絶対必要なのでトレーニングは欠かさず続けていきましょう!

まとめ
いかがでしたでしょうか。
今回は、一点突破学習「文章題」をご紹介しました。
テストのスコアに最も影響を与える算数において王者ともいえる「文章題」はやはり強者です。
- 可視化を武器に自分で文章題の弱点を洗い出してみよう!
- 1つ1つの作業はとても地味、省略させないよう鬼の形相で見守ろう!
- はじめる前に一時的なスピード低下の発生を織り込んでおこう!
- 回答スピードを上げる前に正しいフォームを身につけよう!
可視化により自身の思考の流れを振り返れるようになれば、メタ認知の恩恵に預かれます。
1日も早く講義動画で賢くなる「自動運転モード」に入ってください!
特殊算の見分け方や図の使い方についても、今後紹介していきたいと思います。それでは!








