
みなさん、こんにちは!スタッキーです。
約数・倍数の単元に入ってから最小公約数と最大公倍数につまづいていませんか?
これらの問題の攻略には、約数・倍数の意味をよく知るところから始めましょう。
今回は、約数・倍数、そして素数についてまとめてみました。
チートシートもダウンロードできますので活用してみてください!
この記事は次のような人におすすめ!
・倍数と約数の問題でつまづいており点数が伸び悩んでいる
・求める数が大きくなると答えを導き出すのに時間がかかる
・最小公倍数と最大公約数で混乱する子どもを救いたい
約数・倍数問題の対応力を引き上げたい方は必見です!
それではどうぞ!
※当ブログでは商品・サービスのリンク先にプロモーションを含みます。ご了承ください。
小学生がつまづきやすい約数・倍数
中学受験するなら早めに攻略したい
倍数・約数は、中学入試で頻出の単元の1つで、基本から応用まで広く出題されます。
数の性質の基本を問う単元ということもあり、応用問題が試験に出る学校も多いです。
かけ算と割り算ができれば解ける約数・倍数なのですが、子どもには難しいようです。
通常、小学校では5年生で学習する範囲ですが、塾では進みが早く4年生で習います。
中学受験をする場合、ここでつまづくとその先の算数で苦労するのが目にみえます。
5年生からの算数は、これまで習った単元を基にした応用になる内容がほとんどです。
今回の約数・倍数も基本の単元で、小学生がつまづきやすい単元の1つになっています。
さらに5年生は、算数以外の教科の学習の負担が増えてくる学年でもあります。
理科と社会が追加され、算数だけにたくさん時間が避けなくなってきてしまいます。
なので、苦手になる前に、約数・倍数のつまずきを解消していきたいと思います!

約数・倍数に関する用語を頭に叩き込む
約数・倍数の問題では、最小公倍数や最大公約数を求める問題で子供は混乱します。
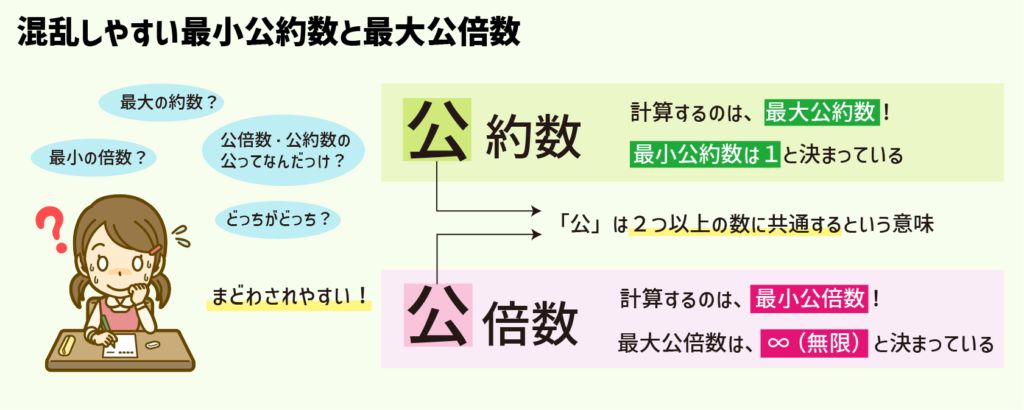
最大や最小、さらに公倍数や公約数という言葉に惑わされてしまい手が止まります。
わが家も、言葉の意味がわかっておらず、何を計算すればいいのか迷子な状態でした。
なので、まずは倍数とは?約数とは?を頭に叩き込んで対象の数1つからはじめました。
そして、対象の数を2つにした時に公倍数と公約数の言葉の意味を理解していきました。
公倍数や公約数の「公」というのは、2つ以上の数に共通するという意味です。
2つ以上の数に共通する数で、最も大きい倍数が最大公倍数、約数が最大公倍数です。
2つ以上の数に共通する数で、最も小さい倍数が最小公倍数、約数が最小公倍数です。
一気に教えると混乱するようなので、1つ1つ問題を解きながらすすめていきました。
子どもに説明していてもすぐに忘れてしまうので、チートシートにしてみました。
チートシートにすることですぐ要点や解き方を思い出せるかなと思いました。
同じことを何度も説明するのも大変だったのでチートシートは省エネにもなります。

最小公約数と最大公倍数に慣れよう
①最大公約数はアイ型(I)で計算する
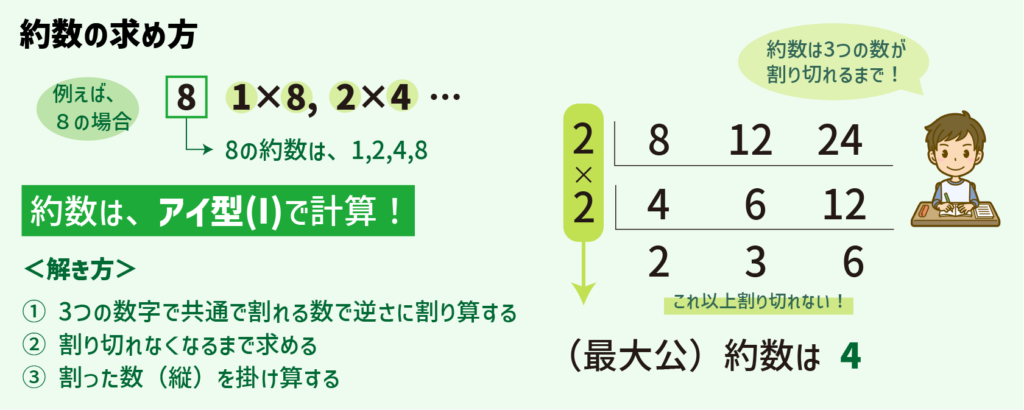
約数とは、対象となる数を割り切ることのできる数のことです。
対象となる数が8の場合、割り切ることができる1、2、4、8が8の約数となります。
2つ以上の数に共通する約数、公約数を知りたい場合には逆さ割り算を使って求めます。
全ての数が割り切れるまで計算したあと割った数の縦をかけた数字が最大公約数です。
図の例では、18と36と54のを逆さ割り算し、3つの数の最大公約数は18とわかります。
最大公約数を求める時は、アイ型(I)で計算する!とわが家では命名しています。
約数では、最小公約数を求める問題はほぼ出ません。1と決まっているからです。
対象となる数に共通する最大の約数(最大公約数)を求められることが重要です。
わが家でも、言葉が意味がわからず何を求めれば良いのか混乱することが多かったです。
最大公倍数や最小公倍数の言葉の意味や、算出方法をチートシートにまとめました。
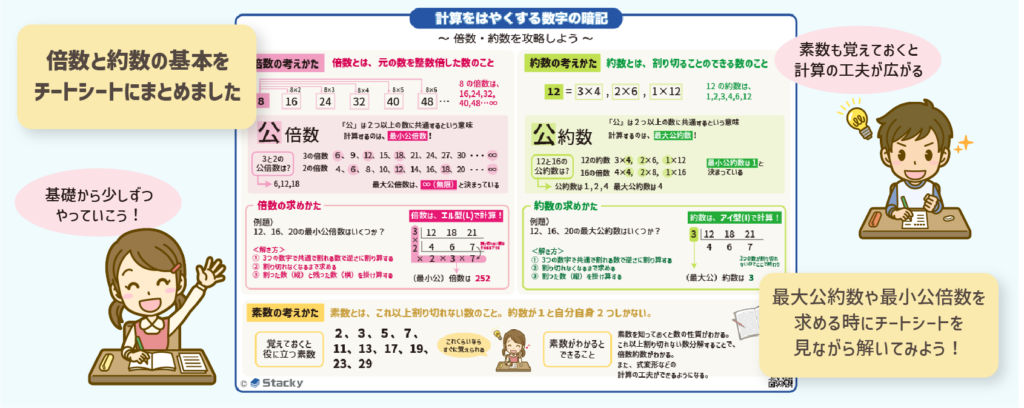
②最小公倍数はエル型(L)で計算する
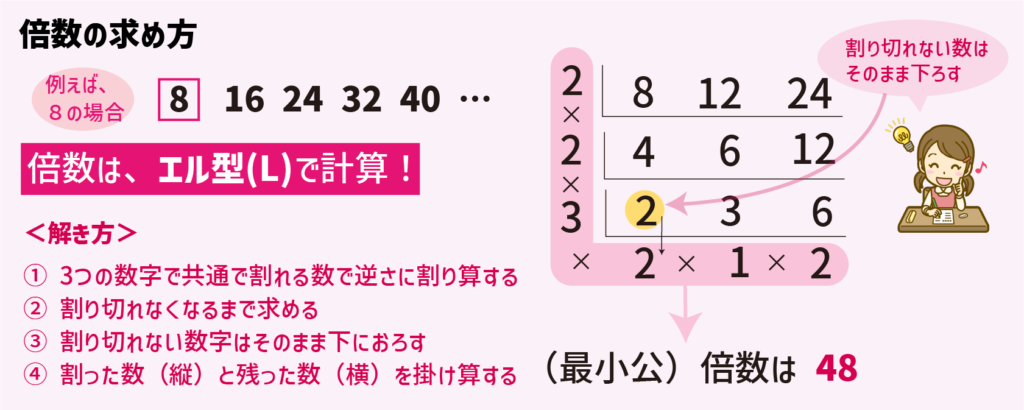
倍数とは、もとの数を整数倍した数のことです。
もとの数が8の場合、16、24、32、40…が8の倍数となります。
2つ以上の数に共通する倍数、公倍数を知りたい場合には逆さ割り算を使って求めます。
逆さ割り算で全ての数が割り切れる、もしくは2つの数が割り切れるまで繰り返します。
割り切れなくなるまで割り算したら、縦と横の数字をかけて出た答えが最小公倍数です。
図の例では、12と18と21の3つを逆さ割り算します。3で割れるので4、6、7となります。
4、6、7のうち、4と6は2で割れます。しかし、7は割れないのでそのまま下におろします。
これ以上割れなくなったので、最後に縦と横を計算して252が最小公倍数になります。
最小公倍を求める時は、エル型(L)で計算する!とわが家では命名しています。
倍数では、最大公倍数は無限∞にあります。なので、試験では最大公倍数は出ません。
対象となる数に共通する最小の倍数(最小公倍数)を求められることが重要です。
③素数は覚えておいて損はなし

素数は、これ以上割り切れない数で、約数が1と自分自身2つしかない数のことです。
素数は数の性質の問題を攻略する上で、その意味や役割を知っておく必要があります。
中学受験では、まずは30までの素数を覚えておくと数の性質がつかみやすくなります。
30までの素数は、2、3、5、7、11、13、17、19、23、29です。覚えちゃいましょう。
ちなみに、1は素数ではないので注意しましょう。理由は、約数が2つないからです。
素数を知っておくと数の分解が早くなり、どんな数で割れるのかがすぐにわかります。
約数がこれ以上ないかどうかを確信できるので覚えておいて損はないです。
まずは基本的な問題をチートシートを見ながら計算し、問題数をこなしていきました。
最小や最大、公倍数や公約数の意味や何が求められているのかが理解できてきます。
さらに、時間をはかってサクっと解けるようにたくさん解いて自信をつけていきます。
倍数や約数の問題をみて、「ああこれね。」と子供が言えるようになったら成功です。
5年生初期の算数でつまずくのが倍数・約数です。ぜひここで基本を固めたいところです。
まとめ
いかがでしたでしょうか。今回は、「約数・倍数」をご紹介しました。
約数・倍数は、中学入試で頻出の単元です。ここで確実に点数をとりたいところです。
ぜひこの機会に学んで、得意科目にしてしまいましょう!
これらは計算時間を短縮してくれる数字なので、ぜひこの機会に覚えてしまいましょう!
- 最小公約数は1、最大公約数は、アイ型(I)で求める
- 最大公倍数は無限、最小公倍数は、エル型(L)で求める
- 素数を知っておくと倍数と約数の分解が早くなる
チートシートでコツをつかんで問題を解けるようになりましょう!
チートシート「倍数・約数」のダウンロードはこちら(無料)今後も算数系チートシートを増やしていきたいと思います。ご期待ください!







