チートシート：多角形の攻略ポイントは内角と対角線！｜ Stacky スタッキー〜子どもたちの学習効果UPをねらうブログ〜

みなさん、こんにちは！スタッキーです。

平面図形に多角形が出てくるとどこから手をつければ良いかわからなくなっていませんか？
今回は、覚えておくとよい多角形の性質について触れてみたいと思います。

スタッキー

この記事は次のような人におすすめ！
・多角形の角度をスラスラと使えるようになりたい
・公式の丸暗記という危ないカケが自分には合わない　　　　　　　　　　　

この記事を読むと、多角形の性質がわかり、解き方に集中できるようになります。

平面図形や規則性の対応力を引き上げたい方は必見です！
それではどうぞ！

※当ブログでは商品・サービスのリンク先にプロモーションを含みます。ご了承ください。

出題頻度が高くない多角形を記憶できますか？

多角形の図形問題が苦手で弱点になっている

問題の中で図形が発しているヒントを捉えきれず、点数を落としてしまっていませんか。

出題頻度がそれほど高くない多角形の問題を暗記のみで乗り切るのは厳しいかもしれません。
図形の基本や性質を理解すれば、少しずつ解き方が見えてきます。

多角形では内角や対角線がよく使われます

多角形の問題は、テストでたまに見かけます。
しかし、わたしは公式を丸暗記していたので、問題を解くときにうまく活用できずにいました。

また、図形の性質そのものを理解していなかったので、忘れたら一貫の終わりでした。
そこで、内角や対角線などの多角形の基本的な性質を効率よくおさえたいと考えたのです。

多角形の内角と対角線をマスターしよう

図形は頂点と辺の数でできている

図形になるまでの成り立ちを考えてみると、まずは点があり、辺ができ、そして面になります。
最初にでてくる面は三角形で、それ以降の多角形にも共通した性質があります。

そのため、多角形を最小単位である三角形の組合せとして認識する方がスッキリします。
手を動かしてみれば一目瞭然ですが、頂点から「２」を引くとこの三角形の数がでてきます。

チートシート「多角形の基本」のダウンロードはこちら（無料）

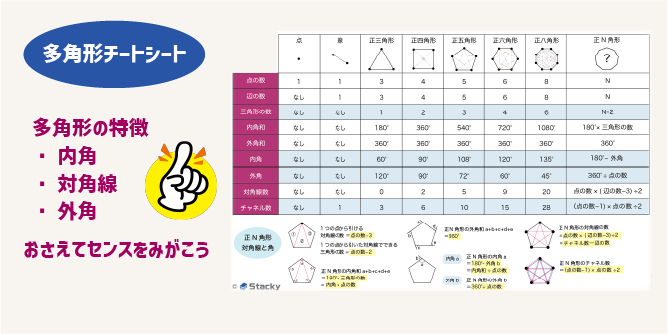
テストによくでる多角形を表にまとめてみました。
まずは、点、辺、面の最小単位である三角形の数を中心に確認してみてください。

多角形の基本は内角和と外角和

チートシートを使いながら、多角形の性質について親子で流れで整理してみました。

まずは、多角形の１つの頂点から対角線を引くと点の数から３を引いた「N-3」になります。
点はそれ自身に線を引くことができず、両どなりの２点には辺しか描けないからです。

つぎに、多角形は前述の対角線に１を足した数である「N-2」の三角形に分割されています。
この三角形の数に180°をかけると多角形の内角和「180°×（N-2）」がでてくる流れです。

そして、内角和を点の数（角の数）で割ることで１つの内角がでてきます。なるほど。

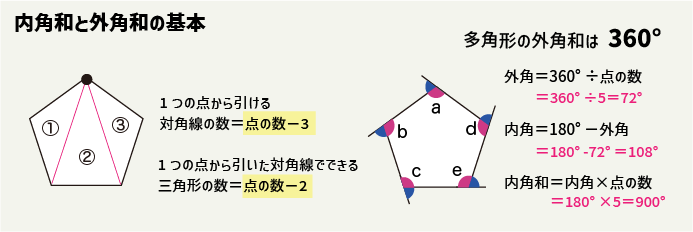
多角形の外角和は常に360°です。この性質を利用して内角を求めることもできます。

つまり、外角＝360°÷点の数、内角＝180°－外角、内角和＝内角×点の数、ともいえます。
正直、コッチの方がラクな気がします。

多角形のチャネル数と対角

多角形の１つの点からほかの点に引ける線の数は点の数から１を引いた「N-1」になります。
これを点の数だけ引くとすべての点がお互いに２本の線で結ばれることが分かります。

つまり、多角形のすべての点を結んだ線の数はその半分の「N×（N-1）÷2」となります。
これは、複数人で会話するときの組合せの数であるチャネル数としてよく登場します。

チャネル数は辺を含んでいますので、対角線の数は「N×（N-1）÷２－N」となります。
もう少し、式を整理すると「N×（N-3）÷２」とも言えます。