
みなさん、こんにちは!スタッキーです。
学習を進めているとニガテ意識が生まれることはありませんか?
わが家では「場合の数」がその危機にあり、テストのたびにイヤな気持ちになっていました。
しかし、頻出分野なら尚更しっかり理解してサクサク問題をときたいと思いませんか。
今回は、わが家で実施した一点突破学習「場合の数」についてお伝えしたいと思います。
この記事は次のような人におすすめ!
・問題用紙を「樹形図」でびっしり埋めつくすわが子を救いたい
・テキストの知識だけで問題がトケルという迷信を捨てられる
・多くの子どもがニガテ意識を持つこの分野を絶対領域にかえたい
・成功体験の蓄積がトップレベルの判断力を生むと信じている
論理的思考で「場合の数」に取り組みたいと考えている方は必見です!
それではどうぞ!
※当ブログでは商品・サービスのリンク先にプロモーションを含みます。ご了承ください。
わたしが「場合の数」にニガテ意識を持つまで
小さな数字と樹形図がもたらす悪夢
和の法則、積の法則、順列、組合せ、樹形図、ベン図、色々な知識があることは分かります。
しかし、どの知識をどのような状況で適用すべきなのかという本質はあまり説明されません。
このような状況にあって、塾や学校の授業に圧倒的な回数登場するのが「樹形図」です。
その結果、子どもに「場合の数=樹形図」というなぞの思考回路が形成されていきます。
小さな数字で教える授業ではすべてのパターンを樹形図で書き出せるので問題に気づきません。
しかし、試験会場で目にする問題は数字が「樹形図」でどうにかなるレベルではないのです。
そして、暗黒の司令塔から聞こえる「樹形図」という言葉に従って地獄の写経がはじまります。
ふと気づけば、問題用紙はあっという間に「数字」と「棒」と「涙」で埋まるのです。
かしこい子は本当にこんなことをやっているのだろうか?それがわたしの感じていたことです。
問題のバリエーションが打ち砕く自信
場合の数がニガテであっても特定のパターンの問題にはなれてくることがあります。
たとえば、低学年のころから試験に登場する数字のカードや経路の問題です。
しかし、そんな自信をいとも簡単に打ち砕くほど「場合の数」はバリエーションが豊富です。
そして、出題者は学習中に出会わなかった問題をあざわらうように狙い撃ちしてきます。

1つ潰しても次が、また1つ潰しても次が、とやっている内に遂にニガテ分野になりました。
このようなドロ仕合から抜け出せるのなら、多少の苦労はしてもよいと思ったものです。
なぜなら、場合の数はレベルの高い試験に100%登場するといっても過言ではないからです。
今になって考えると最初に解法が頭に浮かばない時点で負けていた気がします。
そこで、「秒で解法をみつけられないか」と考えたのです。それがこの実験の主旨です。
シンプルな考え方で「場合の数」を理解する
ムリに小学生に合わせた公式を捨てる
まずは、重要な2つの概念「並べ方&選び方」をイメージで理解してみることにしました。
ただし、小学生の学習範囲にあわせた覚えにくい公式はできるだけ排除することにしました。

理由は「N」だらけの公式が図形等にも登場し、覚えても混ざるのが目に見えていたからです。
公式という危うい知識を排することは、スコアを確実に上げるために良いとも思いました。
並べ方(P):いくつかのものを順序を考えて並べたもの(区別する)
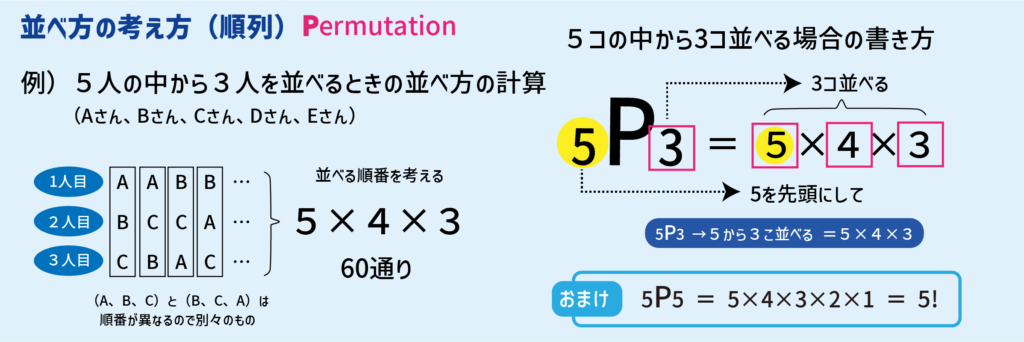
選び方(C):並べる順序を考えずに選んで一組にしたもの(区別しない)
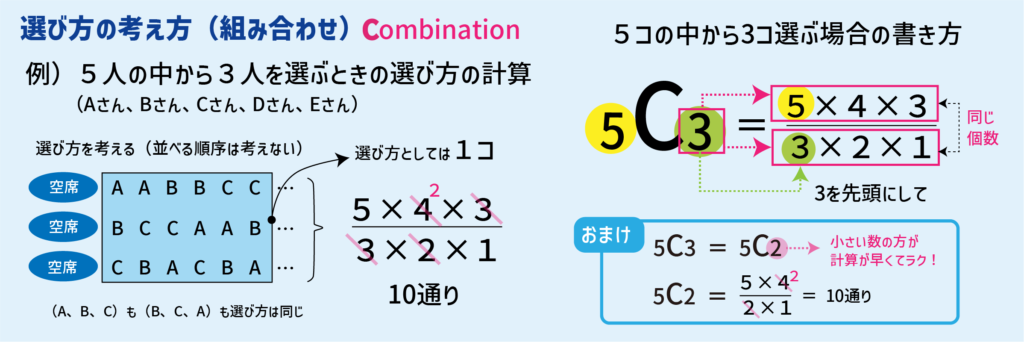
並べ方&選び方の区別

問題の区別に応じて上記の知識を適用できるか、1問ずつ確認していくことにしました。
この段階ではトケル必要はなく「並べ方」か「選び方」かを区別できればOKとしました。
なぜなら、この判別を間違うともはや後の工程をいかにがんばっても答えが合わないからです。
いくつかの問題を切り抜いてカード形式で質問を繰り返していきます。
何回かやってみると本人も特徴のつかみ方に慣れてくるようです。
 ボヤッキー
ボヤッキー 自分が今までわからなかったことが今回の説明で解き明かされていくイメージ
入れ替えたら違うものは、区別アリの(P)だよね
たぶん、あってます。たぶん。
前提条件の処理方法を整理してみる
次は問題の難易度を引き上げている要素の1つ「前提条件」を理解していくことにしました。
オーソドックスな並べ方&選び方の問題も前提条件が変わると急激にムツカシさを感じます。
そして、対処法を知らなければ、あっという間に「樹形図地獄」に引きずり込まれるのです。
この壁を乗り越えるため、出会った問題に含まれる条件を書き出すことにしました。
- 「~が隣り合う」:~を含むカタマリの中を考える、カタマリと他の要素を考える
- 「~が隣り合わない」:~ではない要素を固定してスキマを考える
- 「特定の~を選ぶ」:~を除いて考える
- 「少なくとも~」:全体からすべて~でない場合を引く
- 「同じものを含む」:区別できないものは並びが関係なくなるのでN!で割る
- 「重複を許して~」:選択肢が減らないので階乗ではなく累乗になる
- 「重複を許して~、選ばれないものがあってもよい」:仕切りを使って考える
- 「モノ・ハコの区別なし、個数不定」:すべて書き出す
この活動で並べ方や選び方がどうしてむつかしくなるのかが少し分かってきました。
なぜなら、似た問題でも解き方がまったく異なるという事実を知ったからです
ココでは、問題文から上記のパターンを特定して発話するトレーニングを行いました。
具体的には、問題文を数秒見せて即座に上記のパターンを言い当てるというものです。
言い当てる際は、トナリアウ、トクテイなどの呼びやすいあだ名をつけてみました。
問題のバリエーションと注意事項を知る
これまでの学習でオーソドックスな並べ方と選び方の問題に免疫力がついてきたと思います。
今度は、問題のバリエーションに慣れていきましょう。
ココでは最短経路の問題を例に実験の概要をお伝えしたいと思います。
最短経路の問題には、主に平面と立体の2種類が存在します。
基本的には、たて(↑)・よこ(→)・たかさ(↗)などの矢印をすべて並べるものです。
しかし、同じ矢印の組合せは1つと数えるため、重複を排除する必要があります。
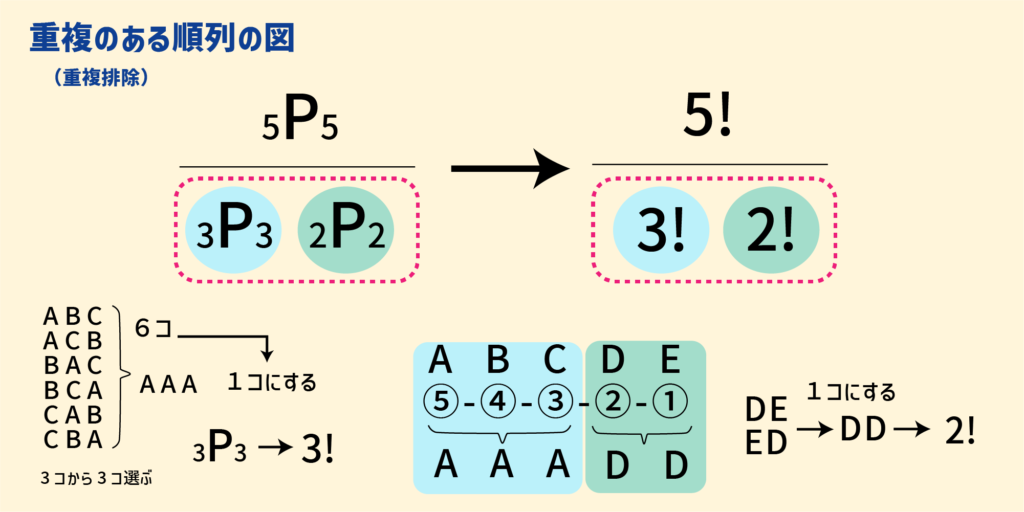
並べ方について反復練習を重ねたのは、このような問題を理解できるようにするためです。
最短経路の問題には主に2つの条件があります。
特定の点を「経由」するパターンと「工事」で特定の経路が通過できないパターンです。
経由のパターンでは、経路を次のように2つに分割して考えていきます。
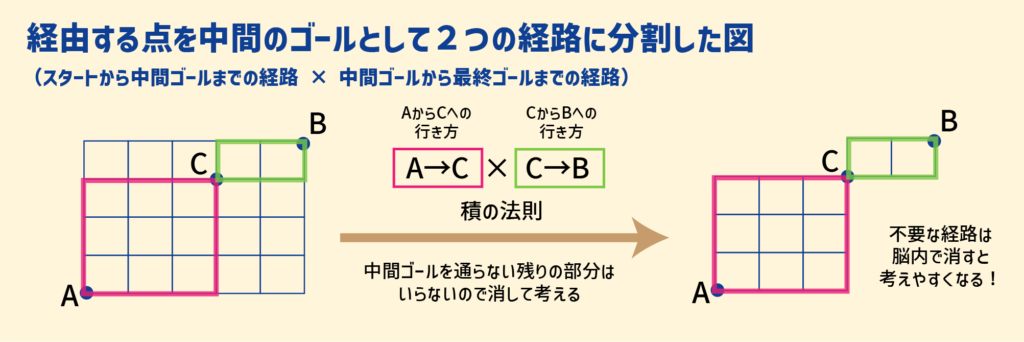
上記の2つの経路の並べ方を積の法則によってかけ合わせて最終的な経路をみちびきだします。
工事のパターンでは、工事箇所を通過する経路に着目して考えていきます。
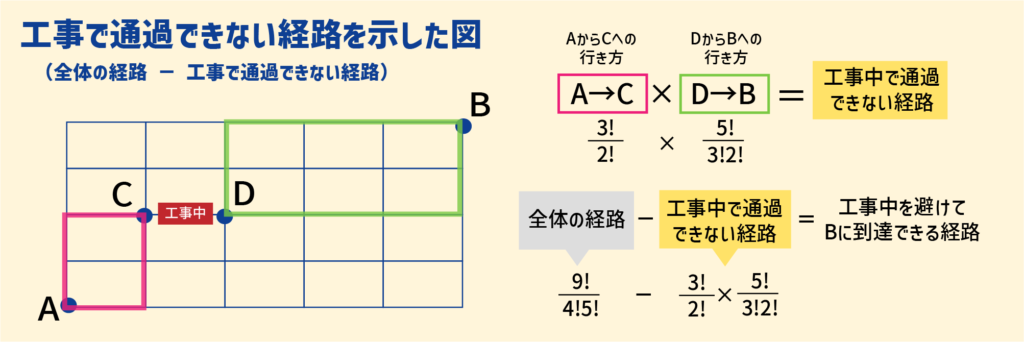
そして、全体の経路から工事で通過できない経路を引いて最終的な経路をみちびきだします。
前述の方法とは別のアプローチにも触れておきたいと思います。
それが、図上の点で経路を足し合わせて書き込んでいく「書き込み方式」です。
この方法は、図の形状が複雑かつ時間に余裕があるときに有効な方法と言えます。
平面の場合は、丁寧に矢印を引きながら数字を合計していけば最終的な経路を求められます。
立体の場合は、図に数字を書き込むとミスが生じやすいので各層を分割した図を用意します。
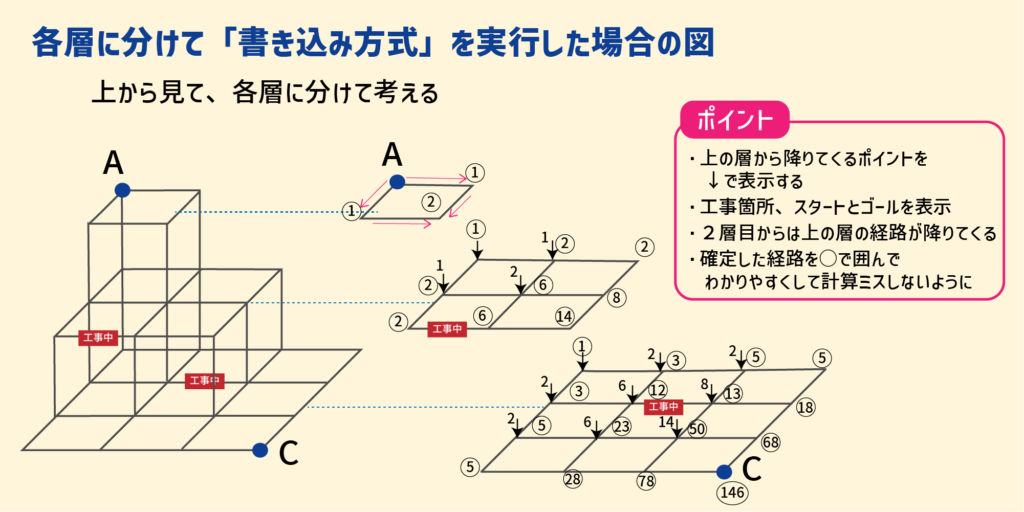
そして「層」ごとに数字を書き込んでいきます。これがミス防止のポイントです。
理由は、図形に数字を書き込むと単純に数字がごちゃごちゃしてくるからです。
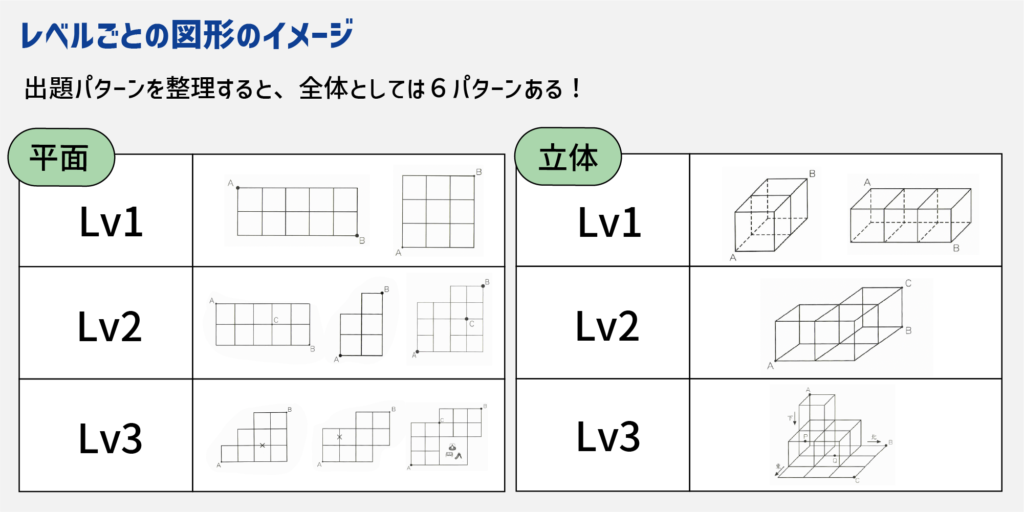
ココまでに登場した出題パターンを整理すると、全体としては6パターンあります。
学習方法は、平面(基本→経由→工事)、立体(基本、経由、工事)とするのがよさそうです。
今回は問題のパターンを言い当ててから問題をトクというステップを踏みます。
問題自体は、テキストと問題集から選定して共通する特徴でグループ化してみました。
 ボヤッキー
ボヤッキー もやもやが消えてきた。
立体は「層」でやったら誰でもトケルよ。きっと。
調子に乗って他のバリエーションも攻略する
ほかにも次のような種類の問題バリエーションに対して同様のステップを踏んでいきます。
サイコロ、コイン、すごろく、赤玉青玉、テーブル、円卓、切り分け
少し持久戦になってきましたが、レベルや種類を分けて解いていけば片付くことは分かります。
テキストや問題集では問題がシャッフルされていますが、グループ化すれば特徴は明らかです。
 ボヤッキー
ボヤッキー ほふゥ~~ンっ!いけんじゃん!
ヨっしゃ!サンジュヨンノゼロロクゴーイチイチ・・・。謎
スッキリとけたという意味だと思いますが、国語に課題アリ!
この記事では、すべてのバリエーションを取り上げることができませんでした。
しかし、問題をグループ化して段階的に理解度を高める効果は絶大だと感じました。
バリエーションごとの対応や問題の選定方法についてもどこかで解説してみたいと思います。
イメージを強化する知識も念のため押さえる
ココまでのように言葉や式でも問題はトケますが、念のため関連する知識もおさえておきます。
ただし、ベン図と樹形図は、他の法則とも関係が深いのでイメージも押さえていきましょう。
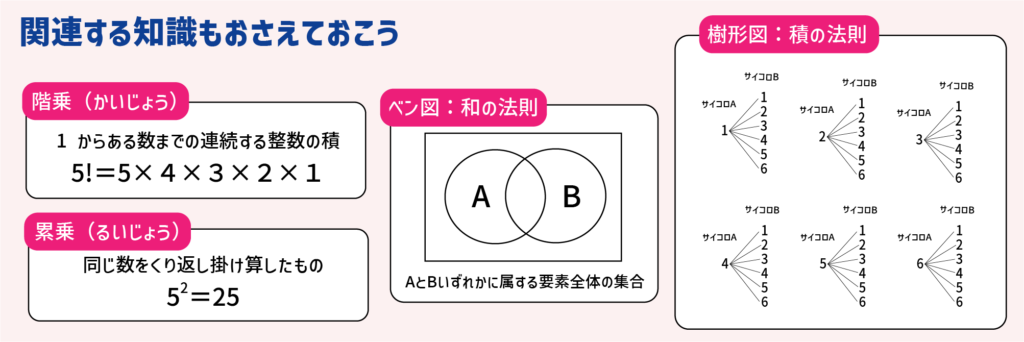
計算を減らすために「階乗と累乗」を覚える
ココまでのトレーニングでパターン認識能力を手に入れた方はいよいよ答え合わせの時間です。
そのために必要なのが「計算」です。しかし、気を抜かないでいきましょう。
場合の数には階乗と累乗が頻繁に登場しますが、ココで計算を間違えては元も子もありません。
そこで、計算しないで九九のようにそのまま答えを出してしまおうと思います。
何度も登場する計算を暗記しておけば、問題用紙がクリーンになることも証明済みです。
今回は「場合の数」において1強ともいうべき「階乗」と名脇役の「累乗」を覚えます。
>>チートシート「階乗と累乗」のダウンロードはこちら(作成中)
トップアスリートの判断力をやしなう
イメージとポイントをサブリミナル!
とうとう一通りの問題パターンを理解して、解法を見出すことができるようになりました。
しかし、ココで終わっては「秒で解法を見つける」という実験の主旨がかないません。
そこで、手に入れた知識を最高速で反応できるところまで引き上げていきたいと思います。
ということで、問題イメージと解法ポイントを書いたカードをループ再生することにしました。
効果があるかどうか分かりませんが、理解した順序で思い出すのにいいかなという感じです。
むかし流行ったサブリミナルに似ているので、悪影響がないか若干心配ではありましたw
ワールド級の試合にチャレンジする
ここまでの実験で当初の目的は十分に達成することができたのではないかと感じています。
しかし、トップアスリートならば、あらゆる場面に秒の思考で対応できてよいはずです!
ということで、過去問にあるアレンジ問題を復習メカニズムに紛れ込ませることにしました。
これは遊び半分ではありません!わが子ボヤッキーをトップレベルの「バアイノカズプレイヤー」にするために仕方なく。
高レベルの封筒問題やタイル問題など、世界にはまだ見ぬ出題パターンがあるのですから。
ということでコッソリ続けて感想をメモしていきたいと思います。
まとめ
いかがでしたでしょうか。今回は、一点突破学習「場合の数」をご紹介しました。
軽い気持ちでフタをあけてしまい、準備に相当な苦労を強いられることになりましたw
- 練習すれば問題に隠されたヒントに秒で反応できるようになる
- 問題用紙を「樹形図」で埋めつくしていた時代がなつかしく思えてくる
- やみくもに問題に挑戦するモヤモヤとした気分から解放される
- はじめて見る問題にも論理的にアプローチしようという気持ちになる
親子2世代で途方に暮れる分野というのは、貴重な体験ともいえます。
ニガテ意識を克服するには、時に立ち止まって考えることが必要なのかもしれません。
テストで手が止まっているのを見かけたら「一点突破学習」を試してみてください。






